Skip to main content

#1. Two Sum | LeetCode Python Solution

Problem​

LeetCode Problem

  1. Two Sum

We will go through 2 Python solutions to the problem and analyze time and space complexity of each approach.

Two Sum - Naive Approach​

Algorithm​

The naive approach uses a nested loop to check if there are 2 numbers in the list that can add up to the target. In addition, it ensures the same element is not used twice.

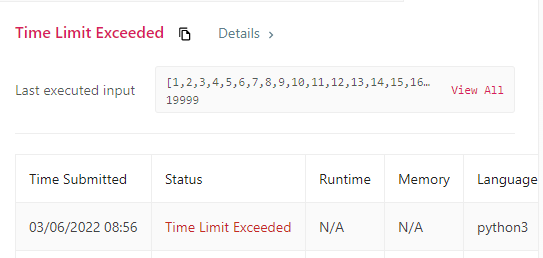
This solution will likely not passing all LeetCode tests as it is not efficient. LeetCode Time Limit Exceeded - Two Sum Brute Force Solution

Implementation​

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        numsLength = len(nums)
        for idx1 in range(numsLength):
            for idx2 in range(numsLength):
                # You may not use the same element twice.
                if idx1 == idx2:
                    continue
                # Return indexes of two numbers in current iteration that add up to target
                currSum = nums[idx1] + nums[idx2]
                if currSum == target:
                    return [idx1, idx2]

Complexity Analysis​

Time complexity: O(n^2).

For each element, we try to find its complement by looping through the rest of the array which takes O(n) time. Therefore, the time complexity is O(n^2).

Space complexity: O(1).

The space required does not depend on the size of the input array, so only constant space is used.

Two Sum - Dictionary Approach​

Algorithm​

We create a dictionary to keep track of visited number as key and its index position as value.

While we are iterating and inserting elements into the dictionary, we check if we have already visited a number that the current number can add up to the target. When we found one, we'll return both number's indexes immediately!

Implementation​

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        # Keep track of visited number and its index position. E.g. {2:0}
        visited = {}
        numsLen = len(nums)
        for currIdx in range(numsLen):
            currNum = nums[currIdx]
            remaining = target - currNum
            # Did we already visit a number that the current number can add up to the target?
            if remaining in visited:
                visitedIdx = visited[remaining]
                return [visitedIdx, currIdx]
            else:
                visited[currNum] = currIdx

Complexity Analysis​

Time complexity: O(n).

We iterate the list with n elements only once. Each dictionary lookup only takes O(1) constant time.

Space complexity: O(n).

The space required depends on the number of items stored in the dictionary, which stores at most n elements in the worst case.